Дроби в картинках

Я не могу писать об актуальном. Но очень соскучилась по друзьям из жж. Поэтому так.

Вчера показывала студенту простейшие фракталы. Просто объясняла, что за фракталы такие. Сегодня один рисунок допилила напильником на совете факультета.

А давайте я вам тоже покажу парочку фракталов?

Фрактал – фигура, которая подобна своей части. Как же так? Как маленькая часть может быть устроена как вся фигура? Оказывается, может.

Один из самых известных фракталов – ковер Серпинского. Возьмите квадрат, поделите его на 9 равных квадратиков и закрасьте центральный.

Оставшиеся 8 квадратиков снова поделите на 9 частей и закрасьте центральный.

И т.д. До бесконечности.

Целый квадрат – точно такая же фигура, как и 8 по краю, только больше в 3 раза. Вот и получается, что вся фигура подобна своей части.

Аналогично можно построить треугольник Серпинского. (Эта картинка из тырнета)

На картинке черный треугольник поделили на 4 равных треугольника, вырезали среднюю часть. С тремя оставшимися сделали так же. И т.д.

Или вот еще очень известный фрактал – кривая Коха. Берем отрезок. Делим его на 3 равные части. Среднюю часть из трех заменяем двумя отрезками (средняя часть и 2 новых отрезка образуют правильный треугольник). Потом с полученными 4 отрезками делаем то же. С полученными 16 отрезками то же. И так далее до бесконечности. (Эта картинка из тырнета)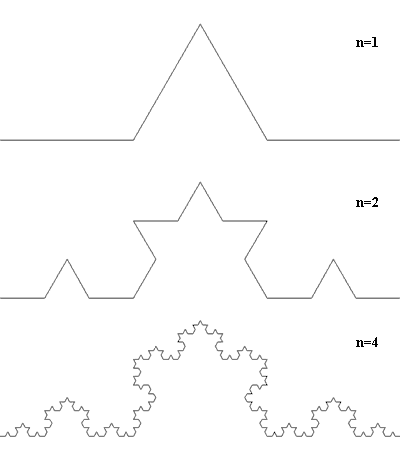

Считается, что некоторые процессы в природе хорошо описываются фракталами. Вот, например, дерево. Палка-палка-палка.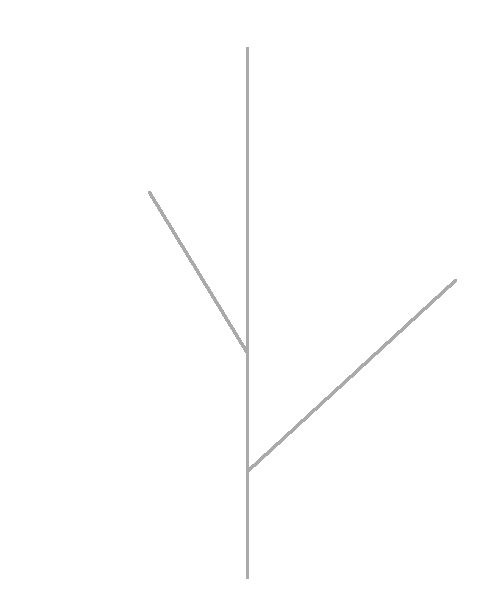

А теперь каждый из трех отрезков (верхний, правый, левый) заменяем на такую же конструкцию палка-палка-палка.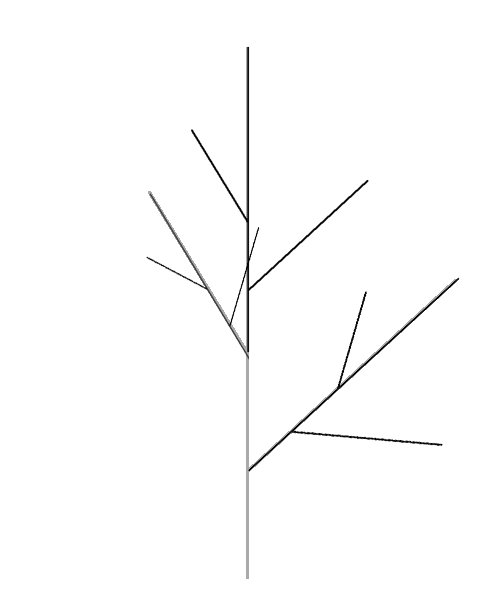

И, как вы уже догадались, снова до бесконечности повторяем процесс.

Вот и дерево. ))

А вот такой красивый фрактал называется Дерево Пифагора. Строится аналогично. (картинка из тырнета)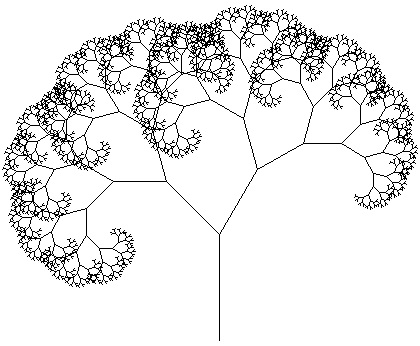

Кому стало интересно, вот тут можно посмотреть красивые фотографии фракталов в природе.

Один из самых известных и красивых фракталов – семейство фракталов Жюлиа. Фракталы Жюлиа трехмерны. Однако если первые 2 координаты – это простые x и y, то третья координата – номер цвета )) Поэтому они такие красивые.

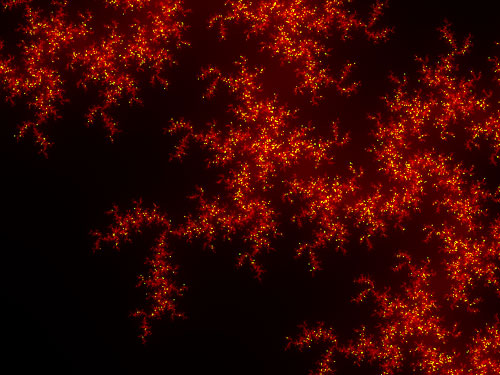
Картинки фракталов Жюлиа получены с помощью программки, которую мы с мужем писали еще студентами. Кому интересно, программка тут. (Там только help в устаревшем формате).

Фракталами можно не только любоваться. Как я уже говорила выше, фракталы иногда описывают какие-то процессы или явления в природе. А в современной науке фракталы активно используются в компьрных науках, в радиофизике и даже в экономике.

Из серии “Математический ликбез”.

• [deleted] 2013-03-22T12:02:28Z

  • kukina_kat 2013-03-22T12:10:50Z

    Фракталы -- вобще прикольная вещь.

• [deleted] 2013-03-22T12:25:25Z

  • kukina_kat 2013-03-22T12:29:23Z

    Смешные эти фракталы.

• [deleted] 2013-03-22T12:40:56Z

  • kukina_kat 2013-03-22T12:42:39Z

    Так и есть. Фракталы -- картинки из раздела "как увлечь ребенка математикой". Как показывает практика, достаточно показать ребенку фракталы, рассказать, что это картинки из математики, и он начинает считать, что математика, наверное, интересная вещь.

• [deleted] 2013-03-22T12:43:36Z

  • kukina_kat 2013-03-22T12:46:34Z

    Одно слово и несколько фамилий математиков ))

• [deleted] 2013-03-22T14:25:19Z

  • kukina_kat 2013-03-22T15:42:01Z

    Мне просто показалось интересным.

    А к тому же, если студент-математик 3 курса не знал такого понятия, то наверняка есть еще масса людей, которые не знают. А так – заинтересуются, возможно что-то посмотрят ))) Узнают, что математика – это не сухарь, а вовсе даже кекс!

    • [deleted] 2013-03-22T17:12:35Z

      • kukina_kat 2013-03-22T17:18:19Z

        ))) Я бы такие посты чаще писала. Просто если я что-то знаю, мне кажется, что это же простая вещь, ее, наверное, все люди знают, чего про нее писать-то?

        Вот недавно прочитала рецепт оладьев - внимание! - из красной икры. Рассказала мужу, поржали вместе. Сразу понятно, что девушка с Дальнего Востока. А есть ли в наших местах что-то, что в других воспринимается аналогично? Думали-думали, не надумали: у нас же все продукты такие обычные. )))

• [deleted] 2013-03-22T15:50:37Z

  • kukina_kat 2013-03-22T16:12:54Z

    Если знаешь, что гуглить, дальше можно и погуглить по слову "фрактал". А когда такого слова не знаешь, так и проживешь всю жизнь, ни разу не увидав.

    Про актуальное в основном грустно.

    • [deleted] 2013-03-22T16:36:59Z

      • kukina_kat 2013-03-22T16:38:18Z

        А тем временем можно порисовать фракталы. )))

• [deleted] 2013-03-22T17:56:50Z

  • kukina_kat 2013-03-23T12:00:36Z

    Фракталы красивые. С детства их люблю рассматривать.

• [deleted] 2013-03-23T08:17:53Z

  • kukina_kat 2013-03-23T11:50:31Z

    Ага. Очень интересная штука. ))

• [deleted] 2013-03-23T12:26:18Z

  • kukina_kat 2013-03-23T15:44:20Z

    А все простое очень-очень сложно ))) Есть такое.

• [deleted] 2013-03-23T16:41:27Z

  • kukina_kat 2013-03-23T18:11:55Z

    Ну, во-первых, "просто описание" -- это уже хорошо. ))

    Если мы описали береговую линию Норвегии как фрактал, то мы можем с большой точностью посчитать ее протяженность или суммарную площадь бухт, например. А если мы не можем описать береговую линию, то посчитать ее протяженность ужасно трудно в связи с ее фрактальной структурой )))

    Или вот описали мы снежинки как фракталы. Или деревья как фракталы. И т.д. Это помогает строить изображение снежинок, деревьев и т.д. в компьютерных играх или в кино при помощи компьютерной графики. Делать их неповторимыми и индивидуальными. Это придает картинке большую степень достоверности.

    А во-вторых, есть другие применения. Например, фрактальное сжатие. Один из самых лучших алгоритмов сжатия! Основан на том, что он файл пытается приблизить фракталом. Ну, а любое сжатие – это очень актуально в компьютерах.

    Еще есть какие-то радио-антенны в форме фракталов, но там я плохо понимаю, чем они отличаются, актуальны ли и т.д.

    • [deleted] 2013-03-24T03:27:26Z

      • kukina_kat 2013-03-24T04:52:31Z

        В том-то и дело, что как раз может. ))) Один из самых классических примеров природных фракталов – норвежские скалистые побережья, фьорды.

        Очень понятно про фрактальную структуру береговых линий написано вот тут (в разделе “Исследования Бенуа Мандельброта” надо читать последний большой абзац).

• [deleted] 2013-03-30T06:18:36Z

  • kukina_kat 2013-03-30T09:32:58Z

    Мне забавно, что такие простенькие незатейливые действия, а приводят к забавному результату (как коврик Серпинского). Множество Жюлиа посложнее, конечно, но зато вобще красота.