Тессеракт и вообще n-мерные кубы

Как только я стала в состоянии после операции читать лекции, первый же вопрос, который задали студенты:

– Когда вы нам нарисуете 4-мерный куб? Ильяс Абдульхаевич нам обещал!

Я помню, что мои дорогие френды иногда любят минутку математического ликбеза. Поэтому кусочек своей лекции для математиков я напишу и тут. И постараюсь без занудства. Лекцию в каких-то моментах я читаю строже, конечно.

Давайте сначала договоримся. 4-мерное, а тем более 5-6-7- и вообще k-мерное пространство нам в чувственных ощущениях не дано. “Мы убоги, потому что всего лишь трехмерны,” – как говорил мой преподаватель в воскресной школе, который первым и рассказал мне, что такое 4-мерный куб. Воскресная школа была, естественно, крайне религиозная – математическая. В тот раз мы вот изучали гипер-кубы. За неделю до этого мат.индукцию, через неделю после этого гамильтоновы циклы в графах – соответственно, это 7 класс.

Мы не можем 4-мерный куб потрогать, понюхать, услышать или увидеть. Что же мы можем с ним сделать? Мы можем его себе представить! Потому что наш мозг гораздо более сложная штука, чем наши глаза и руки.

Итак, для того, чтобы понять, что такое 4-мерный куб, давайте поймем сначала то, что нам доступно. Что такое 3-мерный куб?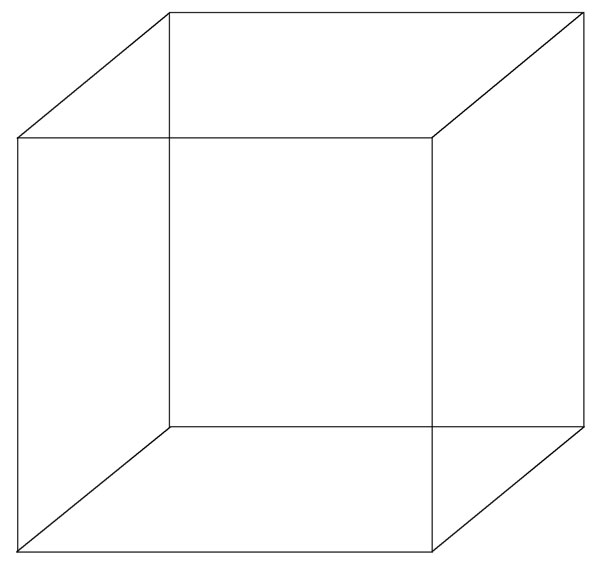

Ладно-ладно! Я не прошу у вас четкого математического определения. Просто представьте себе самый простой и обыкновенный трех-мерный куб. Представили?

Хорошо. Для того, чтобы понять, как же обобщить 3-мерный куб в 4-мерное пространство, давайте сообразим, что же такое 2-мерный куб. Так это просто – это же квадрат!

У квадрата 2 координаты. У куба три. Точки квадрата – точки с двумя координатами. Первая от 0 до 1. И вторая от 0 до 1. У точек куба три координаты. И каждая – любое число от 0 до 1.

Логично себе представить, что 4-мерный куб – это такая штука, у которой 4 координаты и все от 0 до 1.

/* Тут же логично представить себе 1-мерный куб, который не что иное как простой отрезок от 0 до 1. */

Так, стоп, а как же рисовать 4-мерный куб? Ведь мы не можем на плоскости нарисовать 4-мерное пространство! Но ведь 3-мерное пространство мы тоже не рисуем на плоскости, мы рисуем его проекцию на 2-мерную плоскость рисунка. Третью координату (z) мы располагаем под углом, представляя себе, что ось из плоскости рисунка идет “к нам”.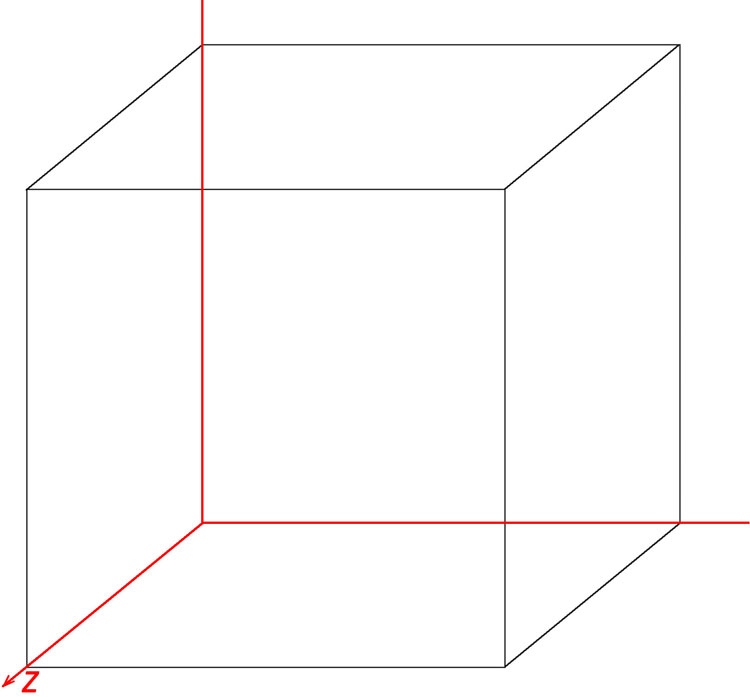

Теперь совершенно ясно, как же рисовать 4-мерный куб. Точно так же, как третью ось мы расположили под некоторым углом, возьмем четвертую ось и тоже расположим под некоторым углом. И – вуаля! – проекция 4-мерного куба на плоскость.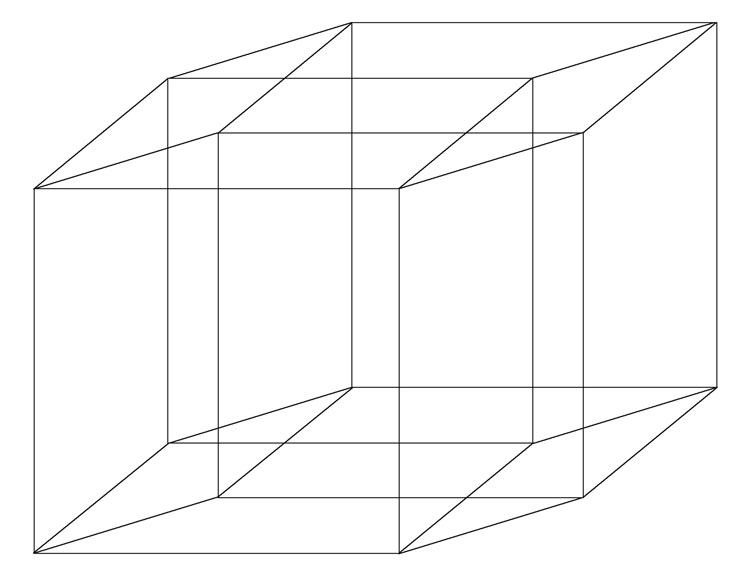

Что? Что это вообще? Слышу я всегда шепот с задних парт. Давайте я подробнее объясню, что же это за мешанина линий. Смотрите сначала на трехмерный куб. Что мы сделали? Мы взяли квадрат и протащили его вдоль третьей оси (z). Это как много-много бумажных квадратов, склеенных в стопку между собой. С 4-мерным кубом то же самое. Давайте четвертую ось для удобства и для сайнс-фикшн будем называть “ось времени”. Нам надо взять обычный трех-мерный куб и протащить его во времени от времени “сейчас” до времени “через час”.

У нас есть куб “сейчас”. На рисунке он розовый.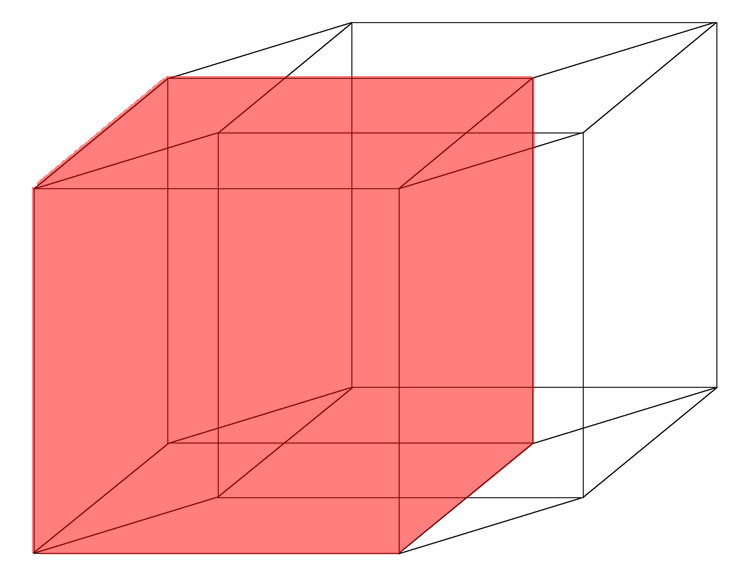

А теперь тащим его вдоль четвертой оси – вдоль оси времени (я ее показала зеленым). И получаем куб будущего – голубой.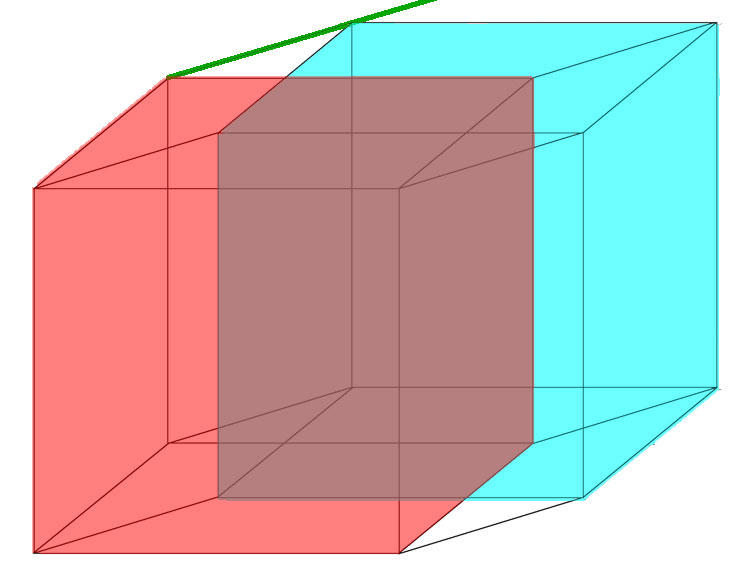

Каждая вершина “куба сейчас” во времени оставляет след – отрезочек. Соединяющий ее теперешнюю с ней же будущей.

Короче, без лирики: нарисовали два одинаковых 3-мерных куба и соединили соответствующие вершины. Точно так же, как делали с 3-мерным кубом (нарисовали 2 одинаковых 2-мерных куба и соединили вершины).

Чтобы нарисовать 5-мерный куб, вам придется нарисовать две копии 4-мерного куба (4-мерный куб с пятой координатой 0 и 4-мерный куб с пятой координатой 1) и соединить соответствующие вершины ребрами. Правда, на плоскости выйдет такая мешанина ребер, что понять что-либо будет почти невозможно.

Когда мы представили себе 4-мерный куб и даже смогли его нарисовать, можно его по-всякому исследовать. Не забывая исследовать его и в уме, и по картинке. Напрмер. 2-мерный куб ограничен с 4 сторон 1-мерными кубами. Это логично: по каждой из 2 координат у него есть и начало, и конец. 3-мерный куб ограничен с 6 сторон 2-мерными кубами. По каждой из трех координат у него есть начало и конец. Значит, 4-мерный куб должен быть ограничен восемью 3-мерными кубами. По каждой из 4 координат – с двух сторон. На рисунке выше мы явно видим 2 грани, ограничивающие его по координате “время”.

Вот тут – два кубика (они чуть-чуть косые потому, что у них 2 размерности спроецированы на плоскость под углом), ограничивающие наш гипер-куб слева и справа.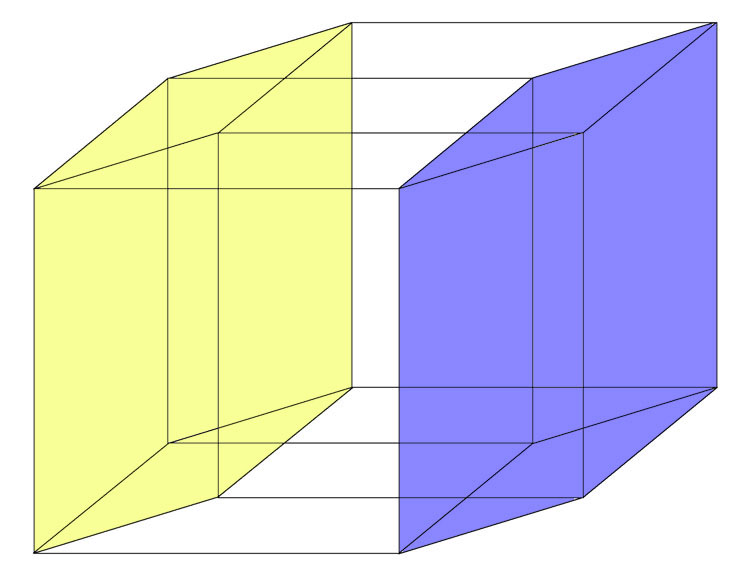

Нетрудно так же заметить “верхний” и “нижний”.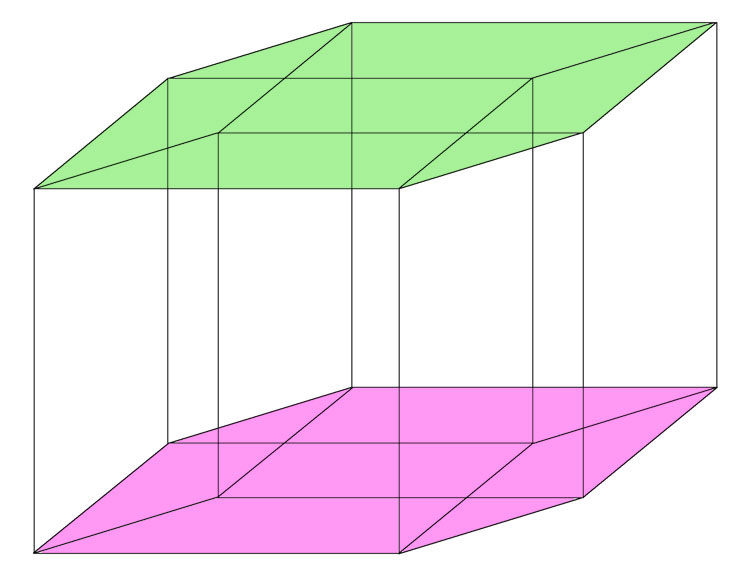

Самое сложное – понять визуально, где “передний” и “задний”. Передний начинается от передней грани “куба сейчас” и до передней грани “куба будущего” – он рыжий. Задний соответственно, фиолетовый.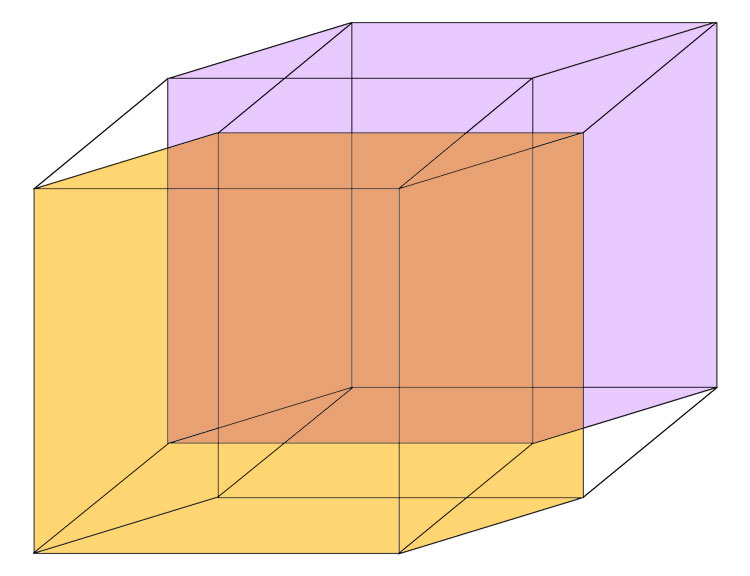

Их труднее всего заметить, потому что под ногами путаются другие кубы, которые ограничивают гипер-куб по другой спроецированной координате. Но заметьте, что кубы все-таки разные! Вот еще раз картинка, где выделен “куб сейчас” и “куб будущего”.

Конечно, можно спроецировать 4-мерный куб в 3-мерное пространство. Первая возможная пространственная модель понятно как выглядит: надо взять 2 каркаса куба и соединить их соответствующие вершины новым ребром. У меня такой модели сейчас в наличии нет. На лекции я студентам показываю немного другую 3-мерную модель 4-мерного куба.

Знаете, как куб проецируют на плоскость вот так. Как будто мы смотрим на куб сверху.

Ближняя грань, понятно, большая. А дальняя грань выглядит поменьше, мы ее видим сквозь ближнюю.

Вот так же можно проецировать 4-мерный куб. Куб сейчас побольше, куб будущего мы видим в отдалении, поэтому он выглядит меньше.

С другой стороны. Со стороны вершины.

Прямо ровно со стороны грани:

Со стороны ребра:

И последний ракурс, несимметричный. Из раздела “ты еще скажи, что я ему между ребер заглядывал”.

Ну, а дальше можно придумывать всякое. Например, как бывает развертка 3-мерного куба на плоскость (это как надо вырезать лист бумаги, чтобы при сворачивании получить куб), так же бывает развертка 4-мерного куба в пространство. Это как надо вырезать кусок дерева, чтобы сворачивая его в 4-мерном пространстве мы получили тессеракт.

Можно изучать не просто 4-мерный куб, а вообще n-мерные кубы. Например, правда ли, что радиус сферы, описанной вокруг n-мерного куба меньше, чем длина ребра этого куба? Или вот вопрос попроще: а сколько вершин у n-мерного куба? А сколько ребер (1-мерных граней)?

Для 4-мерного куба все это можно посчитать на трехмерной модели или на рисунке. Но 5-мерный куб мы что-то рисовать не отважились. Так что придется просто представлять все в уме!

• [deleted] 2018-04-27T06:33:03Z

  • kukina_kat 2018-04-27T09:41:04Z

    Почему же? Нормальный идеальный куб.

    • [deleted] 2018-04-27T09:43:53Z

      • kukina_kat 2018-04-27T09:48:58Z

        Почему же "непонятно"? Куб совершенно понятно, где и "когда". Он занимает все точки из отрезка [0,1] по всем четырем координатам. А никаких других точек не занимает.

        • [deleted] 2018-04-27T09:51:51Z

          • kukina_kat 2018-04-27T10:10:28Z

            Именно. Именно поэтому это не просто куб, а другая фигура -- "4-мерный куб", он же "тессеракт" (хотя я это слово почему-то не люблю).

            Как куб – это бесконечно много копий квадратов, сложенных друг на друга стопкой, чтобы заполнить весь отрезок [0,1] по третьей координате (условно – “по высоте”).

• [deleted] 2018-04-27T06:53:05Z

  • kukina_kat 2018-04-27T09:45:43Z

    Не советую. Не в смысле, что отговариваю, а просто никаких советов не даю. У нас есть другие преподаватели, которые студентам выписывают списки литературы, которые надо прочитать. Я решила, что это не моя фишка. )))

    Я, конечно, считаю, что каждый приличный человек должен в своей жизни прочитать много Хайнлайна (а еще много Азимова, много Бредбери, и Стругацких всё-всё). Но помалкиваю.

  • kukina_kat 2018-04-27T09:51:38Z

    >ага, большое впечатление производит тот факт, что в гиперкуб c ребром 1 можно запихать сколь угодно длинный отрезок, взяв достаточно большую размерность n

    Да, это совершено потрясающий факт!

    Мы много всяких задач про кубы решаем, чтобы отточить всякие знания/понимание многомерной геометрии. Кубы с этой точки зрения проще и понятнее многомерных тетраэдров (их еще иногда называют “симплексы”) и октаэдров.

    • [deleted] 2018-04-27T09:54:40Z

      • kukina_kat 2018-04-27T10:12:12Z

        А по фракталам бывает отдельный спецкурс (не мой). Мои студенты, безусловно, знают, что такое фракталы, но подробно мы их не изучаем – это мимо нашей программы ))

• [deleted] 2018-04-27T08:10:46Z

  • kukina_kat 2018-04-27T09:46:52Z

    Да-да! У нас такое или почти такое постоянно бывает!

• [deleted] 2018-04-27T10:17:49Z

  • kukina_kat 2018-04-27T10:44:26Z

    Читать сложнее, чем слушать. Мелкие (класс 6-7) дети с удовольствием такое слушают и воспринимают. Студенты слушают уже с меньшим восторгом и удовольствием, но все равно слушают и понимают )))

    У детей, кстати, вообще нет какого-то стоппера в понимании. У взрослых так часто бывает: “это физика, это я не понимаю” – и действительно не понимают. А у детей не бывает. Особенно если не говорить им, что вот это – физика, а вот это – лирика. А то обязательно найдутся взрослые, которые им скажут что-то типа “Это мат.анализ, его никто не понимает – и ты не пытайся!"

• [deleted] 2018-04-27T10:19:28Z

  • kukina_kat 2018-04-27T10:40:10Z

    Вот эта дисциплина называется "Алгебра и геометрия". По научному ее надо бы называть "линейная алгебра и аналитическая геометрия".

    • [deleted] 2018-04-27T11:13:12Z

      • kukina_kat 2018-04-27T11:45:08Z

        Там с математикой и связями внутри нее все достаточно непросто. На том этапе развития, который в моем курсе, я показываю студентам, что алгебра и геометрия -- это одно и тоже. Две стороны одной медали. На следующем этапе им опять показывают,что это не так )))

        • [deleted] 2018-04-27T12:07:56Z

          • kukina_kat 2018-04-27T12:53:02Z

            Не, наоборот. Мне кажется, это интересно.

• [deleted] 2025-05-02T00:23:16Z

  • kukina_kat 2025-05-02T00:27:08Z

    Это не параллеььная проекция. Вы слышали звон, да не знаете, где он.

    • [deleted] 2025-05-02T23:49:26Z

      • kukina_kat 2025-05-03T01:30:01Z

        Это в точности центральная проекция в 3-меррое пространство из точки с центральной оси симметрии 4-мерного куба.

        Вы приводите цитату из неграмотной статьи.

        Мне скучно с вами разговаривать. Этот диалог я больше продолжать не буду, ибо сказать мне вам абсолютно нечего.