Блог идеальной жены

Задачки для 8-11

Продолжение позавчерашнего поста с задачками.

От Пирса до Высокой сосны



В бассейне (в стоячей воде) скорость Пети вдвое выше, чем скорость Васи. Но время, за которое Петя проплывает по реке от Пирса до Высокой сосны ровно такое же, какое тратит Вася, проплывая от Высокой сосны до Пирса. Во сколько раз быстрее доплывает Петя от Высокой сосны до Пирса, чем Вася в обратном направлении?

  • Задачу предлагали в 8 классе. Для 8 класса она несложная.

И к ней в пару еще такая задача.

Петя проплывает по реке от Пирса до Высокой сосны втрое быстрее, чем обратно. Он знает, во сколько раз быстрее Васи он плавает в бассейне, поэтому с уверенностью утверждает, что Васе путь туда-обратно и вовсе не под силу. Во сколько раз Петя быстрее Васи в стоячей воде?

  • Вообще, задачи довольно часто придумываются сериями. Считается хорошим тоном, если автор придумал серию задач – то либо взять всю (или почти всю) серию в разные классы, либо же всю серию не трогать. Понятно, почему. Когда ребята пишут параллельно, ничего страшного, что задачи у них похожие. Если же одна из однотипных задач будет использована, то использовать вторую, например, на следующий год уже будет не очень круто.

  • В этом варианте предлагали задачу в 10 классе.
  • Задачи, конечно, похожие, но разные.

Замаскированная теория чисел



В вершинах тетраэдра записали 4 разных натуральных числа. На каждом ребре написали произведение этих чисел. В каждой грани записали произведение трех чисел в ее вершинах. Внутри тетраэдра записали число, равное произведению чисел во всех его вершинах. Все эти числа сложили и получили 2024. Какие числа были написаны в вершинах?

  • Задачу предлагали в 8 классе. Она не сверх-легкая.

  • От числа 2024 решение зависит. Для других чисел будет другое решение.

Классическая геометрия



В трапеции ABCD основание BC вдвое меньше основания AD, а диагональ АС равна боковой стороне CD. Найдите величину угла A трапеции.

  • Задачка для 8 класса.

Однажды в Хогвартсе



Встретились как-то раз три ученика-волшебника из Хогвартса. Белла сказала: среди этих двух нет волшебников. Томми сказал: среди этих двух тут всего один волшебник! А Мина сказала: среди этих двух оба волшебники. А все дело в том, что слизеринцы грязнокровок за волшебников не считают! Кто из детей учится в Слизерине? Кто из детей чистокровные волшебники?

  • Это была самая обсуждаемая задача. Очень долго члены жюри спорили, ведь школьники не знают, и не обязаны знать, кто такой Хогвартс, кто такие волшебники и кто такие грязнокровки. Задача как бы классная, но если начать все пояснять, то становится ужасно длинная.

    В итоге к задачке в конце приписали дисклеймер в виде “Напомним, что Слизерин — это один из факультетов школы магии Хогвартс.” – и задачку со скрипом взяли (см. задачу “Прям как в жизни” из прошлой подборки).

    У школьников не возникло ни одного вопроса к Хогвартсу, волшебникам или грязнокровкам. Только один вопрос: “Мина – это что, женское имя?"

  • Да, имена детей -- тоже с отсылками к книжкам. Но для решения задачи это неважно.
  • Задачу в итоге давали в 9 классе. Только там редакторы варианта решили, что задача понятная. В одном из других вариантов не взяли как раз не потому, что неинтересная, или что-то, а потому что ничего не понятно.

Город Прогрессо



План мексиканского города Прогресо представляет собой пересечение взаимно перпендикулярных прямых – улиц. На всех улицах одностороннее движение. Те улицы, что идут с севера на юг, пронумерованы подряд четными числами. Те, что идут с запада на восток, пронумерованы подряд нечетными числами. Любые две соседние улицы разнонаправлены (движение в противоположных направлениях) и находятся на расстоянии 200 метров друг от друга. Мексиканка Катрина стоит на мотоцикле на углу 51-ой и 60-ой улиц, а ей надо попасть на заправку на угол 53-ей и 62-ой. У нее осталось бензина на 1 км, сможет ли она доехать до заправки?

(аккуратно, тут под спойлером не только рассуждения, но и подсказка к решению)

  • Задача в этой формулировке была в 9 классе.

  • Катрина -- не мексиканское имя. Мексиканский/испаноязычный вариант этого имени -- Каталина. "Ла Катрина" -- это мексиканский вот этот женский скелет к Дню Мертвых, такой нарядный и специфический.
  • Вначале был вопрос: "Какого минимального количества бензина Катрине гарантировано хватит, чтобы доехать до заправки?" -- но решили, что он сильно сложный.

    Не то, чтобы математически сильно сложный. Просто не все дети (и даже взрослые) понимают, что такое “гарантировано хватит”. И опять же, тогда задача получается двухходовка.

  • В 8 классе задача предлагалась в такой формулировке:

    В мексиканском городе Прогрессо все улицы односторонние, и две соседние улицы всегда разнонаправлены. Схема города указана на рисунке (расстояние между соседними улицами всегда 200 метров). Мексиканка Катрина находится на перекрестке и бензина у нее осталось на 1 километр. Но тут она замечает, что по диагонали через площадь от нее находится заправка! Хватит ли Катрине бензина доехать до заправки, соблюдая ПДД?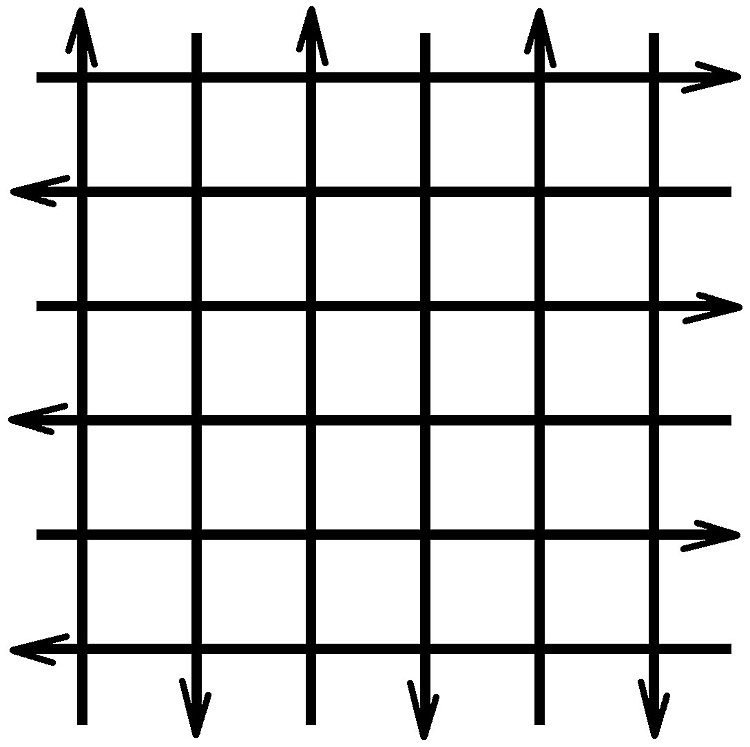

  • В Мексике действительно есть город Прогрессо. Но улицы так пронумерованы не в нем, а в соседнем городе -- в Мериде.

Задача про Суперманзану 28



В равносторонний шестиугольник вписан квадрат так, что две его вершины совпадают с вершинами шестиугольника, а две другие – с серединами сторон шестиугольника. Во сколько раз площадь этого квадрата больше площади оставшейся части шестиугольника?

  • Задачу давали в 10 классе.

  • Можно спрашивать намного более легкий вопрос: какая часть больше, красная или синяя?
  • Задача была в 10 классе.
  • Задача не то, чтобы суперская. Просто мне картинка понравилась. А вот картинка возникла при разглядывании карты нашего города Канкуна в Мексике.
  • В один из младших классов коллеги задачу переделали. Нарисовали рисунок по клеточкам, и спросили немножко другой вопрос (шестиугольник потерял равностороннесть -- ну и черт с ней).

Неопытный доставщик



Приложение доставки Walt рассчитывает время доставки, ориентируясь на среднюю скорость курьера в городе 30 км/час. Неопытный доставщик Оли первые 5 километров доставки проехал со скоростью ровно 30 км/час, но потом на 5 минут застрял на светофоре. С какой скоростью ему нужно проехать оставшиеся 5 километров, чтобы соблюсти время доставки, установленное приложением?

  • Задачу предлагали в 11 классе как не самую легкую. Решили сильно не все.

  • Имя доставщика Оли -- популярное в Мексике мужское имя, сокращение от Оливер. Но в олимпиаде имя просто убрали, чтобы не вызывало вопросы.

  • [deleted] 2024-11-14T18:55:19Z

    • kukina_kat 2024-11-14T19:17:28Z

      Есть решение, в котором ничего перебирать не надо. В 8 классе считается, что теорему Безу и Виета не знают.

      • [deleted] 2024-11-14T19:38:12Z

        • kukina_kat 2024-11-14T19:42:35Z

          В смысле "вряд ли дети до этого догадаются"? Олимпиада уже прошла, дети уже догадались, конечно.

          • [deleted] 2024-11-14T19:47:24Z

            • kukina_kat 2024-11-14T20:35:16Z

              Но это же олимпиадные задачи, не массовые. На олимпиаде бывают задачи, конечно, однотипные с теми, какие уже встречались -- но это не очень хорошо. Как раз весь смысл в том, чтобы придумать задачи не однотипные с теми, что уже были. Как минимум, не однотипные с какими-то задачами, которые школьники могли отработать.

              Да, часто олимпиадность задач зависит от класса, в котором их предлагают (то есть, от предполагаемых методов, которыми владеют дети).

              При этом часто бывает так, что старые олимпиадные задачи входят в стандарт (и, таким образом, со временем перестают быть олимпиадными).

        • [deleted] 2024-11-19T10:07:16Z

          • kukina_kat 2024-11-19T10:09:35Z

            Такое решение и предполагалось для 8-классников. Для 7-классников эта задача преждевременна, в начале года они еще не знают основную теорему арифметики (про разложение числа на простые множители).

            • [deleted] 2024-11-19T10:25:31Z

              • kukina_kat 2024-11-19T11:02:42Z

                Когда я училась, у нас было 10 лет обучения, но последний класс назывался 11. (В середине не было 4-го, мы переходили из 3 сразу в 5). Сейчас этот четвертый класс восстановили. Началку 1-3 растянули на 1-4. Но программа 5 класса теперешнего приблизительно соответствует программе 5 класса, когда я училась. И дальше – тоже все соответствует. Т.е. 8 как мой 8 примерно.

                Но, конечно, я тоже не знаю, что в каком классе проходят. Во-первых, я училась в физ.мат.школе – и мы просто проходили больше, и совсем не в стандартном порядке (кстати, некоторые темы мы проходили чуть позже, чем наши сверстники из других школ). Во-вторых, я, конечно, даже если помню, что квадратные уравнения – это 8 класс, то все равно совершенно не помню, это начало 8 класса, середина или конец. Для олимпиад это важно. У нас в метод.комиссиях обязательно есть школьные учителя математики, которые знают: вот эту тему уже должны были пройти по всем программам. А вот эта тема в некоторых программах есть, в других она только в апреле-мае, поэтому использовать в ноябре ее еще нельзя. Да, мы составляем задачки под программу. Можно, чтобы задачка решалась какими-то еще непройденными темами. Это понятно. Но нельзя, чтобы она не решалась доступными инструментами. Как задачки для 6 класса – обязательно решаются без уравнений. Часто они потому и олимпиадные, что интересно рассуждение без уравнений, а с уравнением там неинтересно совсем.

                Мой папа любил повторять, что алгебра – арифметика для дураков.

                • [deleted] 2024-11-19T18:50:02Z

                  • kukina_kat 2024-11-19T19:17:36Z

                    Мы очень сильно стараемся такого не допускать. Скажем, на ноябрьскую олимпиаду для 8-классников мы даем только темы 7 класса. Темы 7 класса до конца, да, но темы 8 класса не трогаем. Если олимпиада в конце декабря, например, то уже будут темы, которые из текущего класса, но только те, которые есть во всех официальных программах. В России сейчас нельзя работать не по программе, но если когда-то и было можно – это тогда вина учителя, если он программу перестроил, и не подогнал под общее. У нас в школе как раз наоборот: темы, которые могут пригодиться на олимпиадах проходили раньше, а всякие логарифмы и подобную чушь – откладывали подальше, когда олимпиадный сезон кончается.

  • [deleted] 2024-11-14T21:11:47Z

    • kukina_kat 2024-11-14T23:53:44Z

      Да, такая же задача с вопросом "сколько он ждал на светофоре, что понял, что никак не успевает?" -- просто не пошла в олимпиаду. Эта задача и должна была быть легкая. Я ее предлагала для 7 класса, мы ее взяли в 11.

      У нас все равно вечные претензии, что олимпиады сильно сложные выдумываем. Очень много возмущенных родителей. Вот эта задача для 11 класса была третья из шести (по сложности в классической олимпиаде задачи упорядочены). То есть две были легче. Я плохо понимаю, как можно придумать олимпиаду легче.

      А тем более, муниципальная (эта задача предлагалась на муниципальной олимпиаде) – это отбор на региональную. И, конечно, она легче региональной, но она не может быть катастрофически легче региональной, иначе она не будет выполнять свою функцию отбора.

      • [deleted] 2024-11-22T22:51:32Z

        • kukina_kat 2024-11-23T00:32:23Z

          Конечно, ее можно давать в 7-ой. Да даже в шестой. И она легкая, конечно. Но можно давать и в 11-ый. Вообще, в комплекте любой олимпиады (кроме, быть может, заключительного уровня Всероссийской) есть “утешительная задача” – такая задача, про которую составители думают, что ее решат все участники. Вообще, если есть комплект из 6 задач, то мы планируем так: первую решат 100%, вторую 80%, третью 60%, четвертую 40%, пятую 20%, а шестую 0%. Конечно, это не значит, что шестую никто не решит. Возможно, ее решит 1 человек, например. Ну, два. Если в олимпиаде все шесть задач решают несколько человек – это не очень хорошая олимпиада, потому что неудобно детей по местам разводить: кому первое, а кому второе.

          Опять же, ясно, что есть этапы. Первый этап олимпиады (результаты проводятся по районам города или области) – там задачи легче, она совсем простая (кстати, те, кто в прошлом году побеждал на втором этапе, в этом этапе уже не участвуют – сразу идут во второй этап). Эту задачу предлагали на втором этапе, тоже легком (на втором этапе результаты сравниваются внутри области). Третий этап – результаты ребят сравниваются внутри федерального округа, (четвертый этап – последний, финал Всеросса) и ее уже составляет центральная методическая комиссия, а я в местной.

          Ну, вобщем, я к тому, что второй этап – легкий. И эта задача в нем была третьей – и ее примерно 60% и решили.

          Тут вперемешку задачи из двух олимпиад: второй этап Всероссийской и отдельная олимпиада имени Г.П.Кукина – она уровнем почти как третий этап. Задумывалась как тренировка перед 3 этапом Всеросса лет 30 назад. Так примерно и функционирует. А с тех пор, как отменили 3 этап Всеросса для 8-классников, этот самый этап проводят на общественных началах (правда, называют его другим названием) и берут именно нашу эту олимпиаду, которую мы составляем.

          Ну, вобщем, второй этап легче. И эта задача была во втором этапе.

          Сумбурно написала, смешала 2 и 3 этапы в одну кучу, как в посте, так и в комментарии. Но ты умная, разберешься.

          • [deleted] 2024-11-24T18:07:35Z

            • kukina_kat 2024-11-24T18:34:42Z

              Спасибо! Муж тоже говорит, что задачки – так, а его любимая часть про внутреннюю кухню.

              • [deleted] 2024-11-24T20:54:31Z

                • kukina_kat 2024-11-24T22:18:18Z

                  Я знаю, что процессы у нас и в центральном Российском жюри (по математике) построены очень похоже, я там не работаю постоянно, но в целом, кухню знаю. Думаю, что с украинскими коллегами тоже кухня похожая. На самом деле, я ведь с некоторыми шапочно и украинцами знакома, занимающимися подобной деятельностью, а кухня была налажена задолго до того, как все отношения между нашими странами покатились в тартарары. А вот по информатике кухня совсем другая, и структура олимпиады там не очень похожая. Так что там надо как-то отдельно вариться, чтобы разобраться. Но, думаю, готовиться можно и нужно даже без знания кухни (хотя оно полезно, конечно).

  • [deleted] 2024-11-15T16:28:16Z

    • kukina_kat 2024-11-15T19:04:30Z

      Рада видеть такой энтузиазм в решении! Получается, понравилось.))

      • [deleted] 2024-11-15T20:20:00Z

        • kukina_kat 2024-11-15T20:35:02Z

          Выше человек пишет, что теория чисел устная -- на это не надо вестись, это преувеличение. Я не знаю ни одного человека, который ее полностью в мозгу без бумажки решил.

  • [deleted] 2024-11-15T17:02:37Z

    • kukina_kat 2024-11-15T19:03:48Z

      Ого! Геометрию редко у меня в жж решают. Там же не рассуждалка, а именно что чертить, потом что-то считать нужно. )

      • [deleted] 2024-11-15T20:22:56Z

        • kukina_kat 2024-11-15T20:33:11Z

          Да, если брать геометрию -- она до 8 класса приятная, из того, что остается, "когда все забыто" )) Начиная с 9 класса геометрия может быть уже крайне неприятная. Она классная, спору нет. Но обычно на те знания, которые нормальные люди не помнят.

      • [deleted] 2024-11-15T20:46:54Z

        • kukina_kat 2024-11-15T21:15:29Z

          ой, да, очень хорошая игра. И там есть прямо зверски сложные уровни ))

  • [deleted] 2024-11-15T20:41:21Z

    • kukina_kat 2024-11-15T21:19:33Z

      Мина -- это я так Минерву сократила. Родители маглы, насколько я помню, и закончила Гриффиндор. Томми мы больше знаем под именем Том. Самый известный грязнокровка из Слизерина. )) Белла -- это у меня Беллатриса подразумевается.

      Маленькая подсказка для фанатов вселенной )) Но, надо сказать, конечно, она никому еще не помогла!

      • [deleted] 2024-11-16T12:59:45Z

        • kukina_kat 2024-11-16T20:34:25Z

          Скорее, это я их так вольно имена в детские сократила. И, конечно, я далеко не уверена, что они одновременно были школьниками )

  • [deleted] 2024-11-19T12:39:35Z

    • kukina_kat 2024-11-19T13:04:57Z

      Они стоят втроем и каждый говорит про двух оставшихся/думает про двух оставшихся. Не вижу недомолвок, если честно.

    • kukina_kat 2024-11-19T14:08:12Z

      Одно из первых умений, которым учат детишек-олимпиадников: если не понял условия задачи, при малейших разночтениях -- обратись к жюри за разъяснениями. Не ломай голову сам -- на это уйдет больше времени, и скорее всего ты неправильно все поймешь (если уже есть сомнения -- 90%, что ты поймешь задачу неправильно).

      • [deleted] 2024-11-19T18:45:21Z

        • kukina_kat 2024-11-19T19:18:53Z

          Правильно обратилась. )) Вообще, умение задавать вопросы -- отличный навык.